Uday Al-Tamimi

 Uday Al-Tamimi è nato nella città palestinese di Shuafat (شعفاط) vicino a Gerusalemme e aveva 22 anni quando è stato ucciso dai soldati di occupazione israeliani durante la seconda operazione che ha condotto vicino all'insediamento di Ma'aleh Adumim. Uday non aveva precedenti e secondo diverse fonti, non ha affiliazioni organizzative e le indagini israeliane hanno rivelato che i suoi amici che erano con lui in macchina non erano nemmeno a conoscenza di ciò che aveva pianificato. Il quotidiano ebraico Yedioth Ahronoth ha citato fonti della sicurezza secondo cui le valutazioni dei servizi di sicurezza israeliani indicano la possibilità che Al-Tamimi abbia agito da solo, senza alcun collegamento con un'organizzazione palestinese o una cellula organizzata.^[1]

File:ملف:عدي التميمي.jpg

Oday Al Tamimi

assassinio

"Non abbiamo e non temiamo le conseguenze di nulla, guai a chi pensa che abbiamo finito." Un post pubblicato da Uday Al-Tamimi sul suo account Facebook personale il 16 settembre 2022 (ora della Palestina). Dopo diversi giorni di inseguimento, Uday al-Tamimi è tornato per svolgere una nuova operazione contro le forze di occupazione israeliane il diciannove ottobre, che è la seconda operazione compiuta da al-Tamimi in due settimane, ma questa volta le forze di occupazione hanno avuto successo nell'assassinarlo dopo essersi scontrato con loro^[2]. Una telecamera di sorveglianza ha filmato un video che è stato ampiamente diffuso sui social media e mostrava Al-Tamimi che sparava ai soldati di occupazione, e ha continuato a resistere e scontrarsi con loro nonostante le sue molteplici ferite fino alla morte.

قطوع مخروطية متحدة البؤر (Confocal conic sections)

 تسمى القطوع المخروطية "متحدة البؤر"، إذا كان لديها البؤر نفسها. نظرًا لأن للقطع الناقص والقطع الزائد بؤرتين ، فأن هناك قطوع ناقصة أو/و قطوع زائدة متحدة البؤر. عندما يشترك القطع الناقص مع القطع الزائد البؤر نفسها، فإنهما يتقاطعان بزاوية قائمة. وبما أن للقطع المكافئ بؤرة واحدة، ومحور تماثل واحد، فإن للقطوع المكافئة متحدة البؤر محور التناظر نفسه. وبالتالي ، فإن أي نقطة ليست على محور التناظر تقع على قطعين مكافئين متحدين البؤر ومتقاطعان بشكل متعامد.

قطوع مخروطية متحدة البؤر

عندما يكون القطع الناقص والقطع الزائد متحدان البؤر ، فإنهما يتقاطعان بشكل متعامد (بزواية قائمة)

يؤدي سحب مفهوم القطوع المخروطية متحدة البؤر على الفراغ ثلاثي الابعاد إلى الحصول على أسطح ثنائية متحدة البؤر.

يؤدي سحب مفهوم القطوع المخروطية متحدة البؤر على الفراغ ثلاثي الابعاد إلى الحصول على أسطح ثنائية متحدة البؤر. يقال أن اثنين من الاسطح الثنائية متحدة البؤر إذا كان لديهما منحنيات بؤرية مشتركة. 

التي تكون قطوع مخروطية، على وجه التحديد القطع الناقص والقطع الزائد التي ينتميان إلى اثنين من المستويات الرئيسية الثلاثة لتلك السطوح 1

مراجع

1. ^ Theory of principal curvature lines in stone stereotomy- Federico Fallavollita. Marta Salvatore
2. الدكتور حسن العيسوي-Geometric Loci

تبديل

Conjugate diameters of ellipse axes

  الدكتور حسن العيسوي

https://www.researchgate.net/profile/ Hasan-Isawi

Diametri coniugati assi ellisse

Summary

Description	Italiano: Dati due diametri coniugati a' b' costruire l'ellisse delta mediante i suoi assi si presume di aver già determinato i diametri coniugati a' e b' di ellisse delta* e si vuole costruire tale ellisse attraverso il ritrovamento degli assi di delta* per risolvere il problema si considera che tale ellisse delta* e' l'immagine di una circonferenza delta e quindi i diametri coniugati dati a* e b* sono immagini di due diametri della circonferenza ortogonali. per cui secondo tale considerazione si può utilizzare l'affinità (corrispondenza biunivoca con centro improprio) tra l'immagine delta' ed il ribaltamento delta* di delta sullo stesso piano su cui giace delta'. seguendo la figura allegata si può notare quanto segue: l'asse di ribaltamento u coincide con un lato dell'inviluppo dell'immagine delta' . in questo modo si può immaginare che i due diametri a e b nello spazio, rispetto all'asse u, sono rispettivamente, a parallelo ad u e b perpendicolare allo stesso asse u. - per cui il ribaltamento b* del diametro b, e' perpendicolare all'asse u e passa per il punto 0 il ribaltamento d* di una diagonale d di delta passa per il punto 1 (in figura rappresenta il punto d'incontro tra l'immagine d' con l'asse u) e forma 45 gradi l'incontro tra d* e b* individua il ribaltamento C* del centro della circonferenza delta. l'unione tra i punti corrispondenti C' e C* individua la direzione del centro U dell'affinità (in questo caso obliqua rispetto all'asse u) tra l'immagine delta' e il ribaltamento delta* di delta. il segmento C*-C viene considerato come corda di una circonferenza ausuliaria che ha centro nel punto 2 e raggio = 2-C* (uguale anche a 2-C'). in cui il punto 2 e' stato determinato come punto d'intersezione tra l'asse u e l'asse del segmento C*-C'. la circonferenza ausiliaria che passa per i centri C* e C' e interseca l'asse u nei punti 3 e 4. per cui secondo la nota proprietà geometrica della circonferenza, unendo punti 3 e 4 ( che appartengono al diametro u) con i centro C* e C' ( che appartengono al perimetro della stessa circonferenza), si ha due coppie di rette e*-f* e e'-f', che formano tra loro, due a due angoli retti. in questo modo si individuano i cercati assi e' e f' dell'ellisse delta'. e poiché punti corrispondenti ( come 8* e 8') appartengono a rette corrispondenti ( come f* e f') e sono allineati con il centro U, i punti estremi 5', 6', 7' ed 8' degli assi e' ed f', sono determinati rispettivamente come intersezione delle rette parallele alla direzione del cento U e passanti rispettivamente per i punti 5*, 6*, 7* ed 8* con le rette e' e f. العربية: معلوم قطرين متزاوجين لاهليج المطلوب انشاء هذا الاهليج بواسطة محاورة لنفترض انها حددت مسبقا الأقطار المتزاوجة a' b' لأهليج ∆* ونريد انشاء هذا الاهليج عن طريق ايجاد محاوره. لحل المشكلة نعتبر أن الاهليج ∆’ مسقط لدائرة ∆ من مركز لانهائية وبذلك القطرين a' b' هي مساقط قطرين للدائرة ∆ متعامدة على بعضهما. ووفقا لهذا الاعتبار يمكن استخدام التقابل الافيني (تألف بمركز لانهائي) بين المسقط ∆’ وانقلاب الدائرة ∆ على نفس المستوى حيث يوجد المسقط ∆’. بمتابعة الشكل المرفق يمكن ملاحظة ما يلي: محور الانقلاب u يتطابق مع طلع من اطلاع متوازي الاطلاع المحيط الاهليج ∆’. وبهذه الطريقة يمكن تخيل ان الاقطار a b في الفراغ ، بالتوالي ، القطرa' موازي لمحور الانقلاب u والقطر b عمودي على نفس u. لذلك الانقلاب b* للقطر b ، هو عمودي على المحور u ويمر بالنقطة 0 (نقطة تقاطع b مع المحور) والانقلاب d* (لقطر المربع المحيط الدائرة ∆) يمربالنقطة 1 (التي تمثل نقطة التقاء المحور uمع المسقط d' للقطر d) ، ويشكل زاوية 45 درجة مع المحور u. النقطة C* , التقاء الانقلابينd* e b*, تمثل انقلاب مركز الدائرة ∆. الخط الواصل بين النقطتين C* C' ( بالتوالي انقلاب مركز الدائرة ∆ واسقاط نفس المركز) يحدد اتجاه مركز التألف U ( في هذة الحالة تألف مائل بالنسبة للمحور u ) بين الاسقاط ∆' والانقلاب ∆* للدائرة ∆. يعتبر المستقيم C*-C وتر لدائرة مساعدة التي مركزها يقع في النقطة 2 (نقطة تقاطع u مع منصف المستقيم C*-C ونصف قطرها يساوي المستقيم 2-C* (او يساوي 2-C'). محيط الدائرة المساعدة يمر بالمراكز C* و C' ويتقاطع مع المحور u في النقاط 3 و 4. ووفقاً للخاصية الهندسية للدائرة ، بوصل النقاط 3 و 4 (التي تنتمي إلى قطر الدائرة المساعدة) مع المراكز C* e C' ' (التي تنتمي الى محيط الدائرة المساعدة) ، حصلنا على زوجين من الخطوط e*,f* و e',f' التي تشكل فيما بينها، اثنين اثنين, زوايا قائمة. وبالتالي فقد حصلنا على المحاور المطلوبة e',f’ للاهليج ∆' ومنذ ان النقاط المتقابلة (مثل 8 * و 8 ') تنتمي إلى خطوط متقابلة (f* و f') وتستطف باتجاة مركز التقابل U ، فان الاطراف 5', 6', 7' و8 للمحاور e' , f' تحدد كتقاطع بين المحاور e' , f’ مع الخطوط المتوازية لاتجاة U والمارة بالنقاط 5*, 6*, 7* 8* .
Date	5 November 2010, 16:47:31 (according to Exif data)
Source	Own work
Author	Hasanisawi

هذا الرسمة تم إنشائها وتحميلها من قبل المهندس المعماري حسن العيسوي

Questa immagine opera dell'architetto Hasan ISAWI

Sito dell'autore: http://assex.altervista.org/geomtr-1.htm

Autorizzazione accordata : OTRS #2006051010012313

Palestina libera, rivoluzione fino alla vittoria

Ombra propria e portata di una sfera e l'ombra di un punto sulla stessa sfera, in Assonometria cavaliera militare- Shadow proper and range of a sphere and the shadow of a point on the same sphere

   الدكتور حسن العيسوي

https://www.researchgate.net/profile/ Hasan-Isawi

Description	Italiano: Ombra propria e portata di una sfera e l'ombra di un punto sulla stessa fera, in Assonometria cavaliera militare. Una volta che abbiamo finito di rappresentare la sfera in assonometria cavaliera militare ( vedi figura ) e anche il punto P, e stabilita la direzione del raggio luminoso l e la sua prima proiezione l1, passiamo a determinare in ordine: l'ombra del punto P sulla sfera l'ombra propria e portata della sfera L'ombra di un punto P su una sfera si determina come intersezione del raggio luminoso passante per P con sfera. A tale fine si fa passare per il punto P il piano di luce λ, la prima traccia di λ coincide con la prima proiezione l1 del raggio luminoso l, Si determina la sezione circolare Θ tra λ e la sfera. Ma dato che Θ appartiene ad un piano non parallelo al quadro, la sua immagine assonometrica e' un ellisse. La costruzione del quale esige di diversi costruzioni geometriche, per evitare i quali sfruttando la coincidenza tra il quadro con il primo piano di proiezione, conviene eseguire una proiezione ortogonale su un piano verticale parallelo al piano λ e poi eseguire il ribaltamento sul quadro in modo da poter disegnare la circonferenza Θ in vera forma e misura. A tale fine, si stabilisce la linea di terra parallela alla prima traccia di λ; si proiettando i punti d'intersezione della circonferenza equatoriale delta con t'λ, che rappresentano il diametro della circonferenza-sezione Θ. si proietta anche il raggio luminoso l per poter individuare il punto P*2 come intersezione delle proiezione l2 e Θ2, e poi si raddrizza tale punto P*2 e si porta in assonometria per individuare l'ombra P* di P sulla sfera. Con riferimento alla proiezione ausiliaria, le rette P2-P'2 , P2*-P'* e M2-M'2, sono le proiezioni della direzione della corrispondenza tra la seconda proiezione del piano λ ed il ribaltamento della stessa proiezione. Per sapere questa direzione e' sufficiente ribaltare l'asse a nello stesso verso con cui e' stata ribaltata la proiezione ausiliaria di λ. Ovvero il ribaltamento dell'asse a in senso antiorario con cerniera in m1, si seconda coincide con la retta g. per cui e' sufficiente unire l'estremo superiore dell'asse a con l'estremo sinistro del diametro g (con riferimento alla vista assonometrica) per ottenere la cercata direzione di affinità' tra la proiezione di λ ed il suo ribaltamento. la direzione di ribaltamento in questo caso e' obliqua rispetto all'asse che coincide con la linea di terra L.T. . Per determinare l'ombra propria della sfera, si tiene in considerazione il fatto che la separatrice di ombra Σ della sfera, appartiene ad un piano alfa ortogonale al raggio luminoso e passante per il centro della sfera. A tale fine, nella proiezione ausiliaria, si fa passare una retta m2 perpendicolare alla seconda proiezione l2 del raggio luminoso l. La retta m rappresenta la retta di massima pendenza di alfa. Il punto d'intersezione M2 della retta m2 con il contorno apparente della sfera, rappresenta il punto di massima quota della separatrice d'ombra Σ. Il quale può raddrizzato e portato in assonometria. Individuando cosi il punto M che rappresenta in assonometria un estremo di uno dei due diametri coniugati della separatrice Σ. L'altro diametro g passa per C ed e' perpendicolare alla prima proiezione m1 di m. Una volta che si ha due diametri coniugati di un ellisse Σ, e' facile determinarvi gli assi e costruirla (vedi procedimento). Per determinare l'ombra portata della sfera, si stabilisce un piano oggettivo δ su cui poggia la sfera nel punto F ( estremo inferiore dell'asse a della sfera), e si procede a determinare l'ombra m* g* dei due diametri coniugati della separatrice Σ . che in questo caso rappresentano anche gli assi dell'ellisse Σ* ombra di Σ. vale la pena dire che l'ombra portata della sfera sul piano delta corrisponde all'intersezione di questo piano delta con un cilindro di rotazione che ha come sezione retta la separatrice d'ombra Σ ed ha come asse il raggio luminoso passante per il centro della sfera. Concetti Nella soluzione del problema dell'esercizio precedente sono stati affrontati alcuni concetti della geometria descrittiva che di seguito si voglia ripercorrere in modo generale : Figure che non appartengono a piani paralleli al quadro, hanno immagini deformate, che lo studente di architettura deve conoscere a priori. Nell'esempio illustrato abbiamo notato che la circonferenza sigma separatrice d'ombra della sfera appartiene ad un piano generico che non e' parallela al piano di quadro (coincidente in questo tipo di assonometria con pigreco1), per cui la circonferenza proiettata si trasforma in ellisse. c'è da tenere presente che questo caso di deformazione avviene in tutti i tipi di proiezioni cilindriche ( Assonometria, obliqua, assonometria ortogonale, il metodo di Monge) e coniche ( prospettiva). Nel caso dell'esempio illustrato, la circonferenza sigma e' una sezione del piano di quadro con il cilindro proiettante la circonferenza. La quale appartiene ad un piano inclinato rispetto all'asse del cilindro proiettante e ne consegue che esso e' un cilindro ellittico e quindi sezionando questo cilindro con un piano (il quadro) non ortogonale al suo asse, si ha (salvo casi particolari) un ellisse. Riassumendo il concetto: sezionando un cono (incluso il cilindro come cono con vertice improprio) con un piano non ortogonale all'asse si ha una sezione diversa dalla sezione retta di tale cono. La determinazione della vera forma e misura di questa sezione, può avvenire, nel metodo tradizionale, utilizzando ad esempio l'omologia di ribaltamento sul quadro o su un piano parallelo al quadro. Nel metodo della modellazione tridimensionale, dato che e' possibile cambiare con facilita il tipo di proiezione e la posizione del centro di proiezione, e' possibile disporre la figura generica parallelamente al monitor del computer (coincidente con il quadro). Come abbiamo visto nell'esempio, l'ombra del punto P sulla sfera e' un problema d'incidenza tra una retta (raggio luminoso) ed una superficie ( la sfera), la soluzione di questo problema avviene individuando il punto comune P* alla retta l e la sezione della superficie K eseguita con un piano ausiliario lamda passante per la retta l. Questa procedura per risolvere il problema d'incidenza può essere, in generale, applicata alla maggior casi d'intersezione tra retta e superficie. In cui, la retta l può essere immaginaria come il raggio luminoso, una retta proiettante nella corrispondenze affini (traslazione, ribaltamento, rotazione) o nella corrispondenza prospettiva; oppure può essere una retta oggettiva come lo spigolo di una piramide, di un prisma, la generatrice di un cono di un cilindro. Come si può notare nell'esempio, e' stato utilizzato un piano ausiliario verticale lamda per risolvere il problema di incidenza tra una retta l e superficie K. Questo utilizzo, e' facilitato dal fatto che di norma per rappresentare un superficie, nel disegno digitale o in quello tradizionale, si inizia con la prima proiezione ortogonale, per cui e' sufficiente individuare i punti d'intersezione tra la prima traccia del piano verticale e le rette della superficie in prima proiezione; e poi da questi punti, tracciare le verticali che incontrano le relative rette della superficie nello spazio nei cercati punti della sezione. pero c'è da tenere in considerazione che quando si opera in bidimensionale, tale sezione può essere laborioso da costruire perché occorrono altri procedimenti, oltre a quelle citate, come le operazioni di ribaltamento. Per esempio, con riferimento alla figura, la sezione del piano verticale lamda con la sfera e' una circonferenza nello spazio ma la sua proiezione assonometrica e' un ellisse, che e' stato evitato di costruirla facendo l'operazione di ribaltamento della circonferenza, in modo da facilitare l'operazione di individuare il punto d'intersezione P2* tra la retta l e la circonferenza ribaltata. العربية: الظل الذاتي والساقط لكرة وظل نقطة على نفس الكرة في الاكسنومتري الكافاليرا الافقية بمجرد الانتهاء من تمثيل الكرة في الاكسنومتري الكافاليرا الأفقية (أنظر إجراء المرحلة الأولى) ، وكذلك النقطة P ، وتم تعيين اتجاه شعاع الضوء l واسقاطة الأول l1, يمكن متابعة العمليات بالترتيب التالي : ظل نقطة P على الكرة ظل ذاتي وساقط للكرة يتم تحديد ظل النقطة P على الكرة كتقاطع بين الكرة وشعاع الضوء المار بالنقطة P. ولهذه الغاية, نمرر بالنقطة P مستوى ضوء λ . الأثر الأول لهذا المستوى يتطابق مع الإسقاط الأول l1 للشعاع l . ونحدد التقاطع الدائري Θ بين λ والكرة. ولكن بما ان Θ تنتمي إلى مستوى غير موازي لمستوى الإسقاط 1π ، فصورتها الاكسنومترية تكون اهليج. وكما هو معروف رسم الاهليج يتطلب بعض الإنشاءات الهندسية ، فلتفادي هذه الإنشاءات يمكن الاستفادة من خاصية هذا النوع من الاكسنومتري، من خلال إجراء إسقاط مونجي على مستوى رأسي موازي للمستوى λ , ومن ثم نقوم بعملية قلب مستوى الاسقاط المونجي لرسم الدائرة Θ بشكلها ومقاسها الحقيقي. عمليا، نرسم خط الأرض L.T بحيث يكون موازي للأثر الاول t'λ للمستوى λ ، ومن ثم نسقط على L.T نقاط تقاطع ∆ مع t'λ . هذة النقط تمثل قطردائرة التقاطع Θ . نسقط أيضا شعاع ضوء لتحديد نقطة التقاطع P*2 بين Θ2 و L2 . ومن ثم نقوم هذه النقة P*2 لايجاد موضعها الاكسنومتري P* , والتي تمثل ظل النقطة P على الكرة. لتحديد الظل الذاتي للكرة ، نأخذ في الاعتبار أن فاصل الظل للكرة، ينتمي إلى مستوى α عمودي على شعاع الضوء ومار بمركز الكرة. في هذة الحالة, فاصل الظل هي الدائرة Σ والتي تتحول الى اهليج في هذا النوع من الاسقاط الاكسنوكتري. لإيجاد هذا الاهليج Σ, نعمل في الإسقاط المونجي ، بتمرير الخط m2 بشكل عمودي على الاسقاط l2 لشعاع الضوء l. الخط m يمثل خط أقصى ميلان للمستوى α ويمثل ايضاً واحد من الاقطار المتزاوجة للاهليج Σ . نقطة التقاطع M2 بين الخط m2 وكفاف الكرة في الاسقاط المونجي , يمثل نقطة أقصى ارتفاع لفاصل الظل Σ. حيث يمكن تقويم ارتفاع هذه النقطة M2 ومن ثم نقلها الى موضعها الاكسنومتري لايجاد النقطة M التي تمثل طرف القطر m, القطر الأخر g للاهليج فاصل الظل Σ يتطابق مع قطر الدائرة الاستوائية ∆ ويكون عمودي على الاسقاط الاول m1 للخط m. وبمجرد الانتهاء من ايجاد اثنين m و g من الأقطار المتزاوجة, يمكن القيام بالاجراء المفصل في الشكل -- لانشاء الاهليج Σ. لتحديد الظل الساقط للكرة، نفترض وجود مستوى افقي δ حيث ترتكز الكرة في الطرف السفلي لمحورها. نتابع الإجراء بإيجاد الظلال m* g* للأقطار m g . والتي في هذه الحالة تمثل أيضا محاور الظل الساقط Σ* للاهليج Σ. ومن الجدير بالذكر أن الظل الساقط Σ* لكرة على مستوى δ هو تقاطع بين المستوى δ واسطوانة دورا نية مقطعها القائم فاصل الظل Σ ومحورها شعاع الضوء المار بمركز الكرة. تعليق من بين العدد اللانهائي من المستويات المارة بشعاع الضوء والقاطعة سطح متلقي ظل نقطة ما, لقد تم اختيار في التطبيقات السابقة استخدام المستوى الرأسي كعملية مساعدة لإيجاد ظل تلك النقطة. وهذا الاختيار يمكن ان يبرر في الرسم التقليدي (ثنائي الابعاد) وفي النمذجة السلكية وايضاً في النمذجة السطحية, حيث هناك الحاجة الى عمليات من الانشاءات الهندسية للوصول الى ايجاد التقاطع بين مستوى الضوء والسطح المتلقي, والتي عادة ما تكون أسهل باستخدام المستوى الرأسي. بينما في النمذجة الصلبة, بمجرد الانتهاء من انشاء الكيانات الهندسية المطلوبة, يمكن الحصول على ذلك التقاطع بطريقة تلقائي بمجرد تعيين أي مستوى مار بالشعاع وقاطع السطح المتلقي. عملياً ، وبما ان المستوى يحدد ايضاً بتعيين ثلاثة نقاط غير مستطفة على نفس الاستقامة, فيمكن تحديد مستوى الضوء بتعيين نقطتين على شعاع الضوء والنقطة الاخرى في أي نقطه في الفراغ. أستخدام المستوى الرأسي في النمذجة الصلبة أيضاُ, يمكن ان يبرر لسهولة التعرف علية ولأنه يسهل تفسير ومتابعة الانشاءات الهندسية ، وبذلك يسهل قراءة وترجمة الرسم. في حل مسألة المثال السابق لقد واجهنا بعض مفاهيم الهندسة الوصفية التي في ما يلي يراد اعادة سردها بشكل عام: الاشكال التي لا تنتمي إلى مستويات موازية لمستوى الاسقاط π ، لها اسقاطات مشوهة ، والتي طالب الهندسة المعمارية يجب ان يعرفها مقدما. في المثال المعروض (شكل --) لاحظنا أن الدائرة Σ فاصلة ظل الكرة تنتمي الى مستوى مائل بالنسبة لمستوى الاسقاط (متطابق مع الاسقاط الاول المونجي في هذا النوع من الاكسنومتري)، وبالتالي الدائرة تتحول الى اهليج في الاسقاط الاكسنومتري. من الضروري الأخذ في الاعتبار أن هذه الحالة من التشوه تحدث في جميع أنواع الإسقاطات المتوازية (الاكسنومترية العمودية، الاكسنومترية المائلة، وطريقة مونج) والمركزية (المنظور) . الاهليج ‘Σ هو مقطع لإسطوانة اسقاطية أجري بمستوى الاسقاط. رواسم هذة الاسطوانة هي خطوط مارة بمركز الاسقاط اللانهائي وبنقاط الدائرة المسقطة Σ. هذة الدائرة تنتمي إلى مستوى مائل بالنسبة لمحور الاسطوانة ويترتب على ذلك ان هذة الاسطوانة هي اهليليجية، وبالتالي بقطع الاسطوانة بمستوى غير عمودي على محورها ، سيكون لدينا اهليج (إلا في حالات خاصة) . لتلخيص المفهوم : بقطع مخروط (بما في ذلك اسطوانة كمخروط برأس لانهائي) بمستوى غير متعامد على محورة سينتج مقطع مخروطي مختلف عن المقطع القائم لنفس المخروط. كما رأينا في المثال أعلاه ، ظل النقطة P على الكرة هي مسألة تقاطع بين خط مستقيم (الشعاع) وسطح (الكرة) . حل هذه المسألة تكمن في العثور على ألنقطه المشتركة P* للخط l ولمقطع السطح. يمكن أن يتم الحصول على هذا المقطع باستخدام أي مستوى مساعد λ مار بالخط l . هذا الإجراء يمكن تطبيقه بشكل عام على معظم حالات التقاطع بين خط وسطح. حيث الخط l يمكن أن يكون خيالي كشعاع ضوء (كما هو في المثال المعني)، كخط إسقاط في تالف أفيني (انزلاق ، انقلاب ، دوران) أو في تألف منظوري ، أو يمكن أن يكون واقعي كحافة هرم أو منشور, أو راسم سطح مخروطي أو اسطواني. وكما يتضح في المثال ، فقد استخدم مستوى مساعد رأسي λ لحل مشكلة التقاطع بين الخط l والسطح K. لتمثيل سطح ما في الفراغ , في الطريقة التقليدية أو الرقمية, عادة ما يبدأ برسم الإسقاط الأول، وبالتالي يكفي تحديد نقاط التقاطع بين الأثر الأول للمستوى الرأسي والإسقاط الأول للخطوط الهامة التي تمثل السطح، ثم من هذه النقاط ، ترسم خطوط رأسية التي تقابل خطوط السطح في الفراغ وفقاً للنقاط التي تمثل المقطع. ولكن ينبغي الأخذ في الاعتبار أن إنشاء المقطع في حالة الرسم ثنائي الأبعاد, يتطلب الحاجة إلى عمليات إنشاء أخرى ، بالإضافة إلى تلك المذكورة كما هي عملية الانقلاب. على سبيل المثال، وبالإشارة إلى الشكل المعروض، بقطع الكرة بالمستوى الرأسي λ نحصل على دائرة والتي تتحول إلى اهليج في الإسقاط الاكسنومتري. تم تجنب إنشاء هذا الاهليج من خلال إجراء عملية قلب الدائرة على مستوى الإسقاط. والذي يهدف إلى تسهيل مهمة العثور على نقطة التقاطع P2* بين الخط l والدائرة المقلوبة.
Date	13 November 2010
Source	Own work
Author	Hasanisawi

هذا الرسمة تم إنشائها وتحميلها من قبل المهندس المعماري حسن العيسوي

Questa immagine opera dell'architetto Hasan ISAWI Sito: http://assex.altervista.org/geomtr-1.htm

Autorizzazione accordata : OTRS #2006051010012313

Palestina libera, rivoluzione fino alla vittoria

l'ombra di una retta su una superficie conica come parabola - the shadow of a line on a conical surface as a parabola- ظل خط مستقيم على مخروط كقطع مكافئ

   الدكتور حسن العيسوي

https://www.researchgate.net/profile/ Hasan-Isawi

--------------------------------------

Italiano: l'ombra r* di una retta r su una superficie conica K, si determina come parabola d'intersezione del piano di luce passante per r con tale superficie K. Premodellazione Stabilito di volere rappresentare l'ombra parabolica di una retta r su un cono di rotazione K. Le operazioni di premodellazione sono i seguenti: Si disegna una circonferenza ∆ appartenente al primo piani di proiezione come base di K. Si disegna una retta verticale a passante per il centro V1 di ∆ come asse di rotazione del cono K. Si fissa su asse a un punto V come vertice di K. si disegna una generatrice g, di K, passante per il vertice V e per un punto G della base ∆. Per disegnare una retta r nello spazio in modo che sia parallela alla generatrice g, si decide un punto T'r come prima traccia di r e da questo si traccia r1 parallela g1 e r parallela a g. Si traccia una retta verticale da un punto P1 di r1 e si individua il punto P come intersezione con r. Per determinare il raggio luminoso l si considera r come retta di massima pendenza del piano di luce passante per r . Per cui la prima traccia del piano passa per T'r ed ha direzione perpendicolare ad r1. Poiché l'ombra di una retta su un piano coincide con la retta d'intersezione tra il piano di luce passante per r con tale piano che riceve l'ombra, per cui in questo caso la prima traccia t'λ del piano di luce λ coincide con l'ombra r* di r su π1. In ultimo si decide P* su t'λ e si unisce con P individuando la il raggio luminoso L. La prima proiezione l1 del raggio luminoso si individua unendo P1 con P*. Modellazione in questo cono si procede alla generazione del modello del cono e quella delle ombre. Si sceglie il triangolo VV1G come figura generatrice e la retta V1-V come asse di rotazione. Si genera l'ombra della retta e del cono scegliendo la retta P-P* come direzione di una sorgente di luce impropria. Analisi concettuali e tecniche A questo punto, dopo che abbiamo finita di preparare i modelli componenti l'esercizio in questione, si passa alla ultima fase quella di analizzare i concetti e le tecniche riguardanti le ombre generate. Le coniche La parabola si ottiene sezionando un cono quadrico con un piano parallelo ad una generatrice del cono. In questo caso per ottenere un ombra parabolica della retta r su un cono K, bisogna che il piano di luce sia parallelo ad una generatrice di K. Per verificare il parallelismo del piano con una generatrice del cono, si fa passare per il vertice del cono un piano ausiliario gamma e secondo la giacitura di gamma rispetto alle generatrici del cono, la sezione può essere, rispettivamente: -un ellisse, se gamma non e’ parallelo a nessuna generatrice; significa che λ seziona tutte le generatrici del cono in punti propri dell’ellisse. Una parabola, se gamma e’ parallelo ad una generatrice. significa che λ seziona tutte le generatrici in punti propri meno una che la incontra in un punto improprio. Il Quale rappresenta la direzione dell’asse della parabola. Una iperbole se gamma e’ parallelo a due generatrici. questo significa che λ sezione tutte le generatrici del cono in punti propri meno due generatrici che li incontra in due punti impropri che rappresentano le direzioni degli asintoti dell’iperbole Parallelismo retta e piano l'ombra di una retta su un cono e' parabolica se il piano di luce λ passante per la retta r risulta parallelo ad una generatrice del cono. Si tiene presente che un piano λ e’ parallelo ad una retta g se λ contiene una retta r parallela alla retta g. In questo caso, si vuole costruire un piano di luce parallela alla generatrice g del cono. A tale fine si prende un punto P del raggio luminoso l e per esso si fa passare una retta r parallela alla generatrice g. La prima traccia di λ (coincidente con l’ombra r* di r) si individua unendo la prima traccia T’r di r con la prima traccia P* del raggio luminoso l. Punti notevoli Per determinare il vertice della parabola si fa passare per l’asse del cono un piano β in modo che sia perpendicolare al piano di luce λ. A tale fine, per V1 si fa passare la prima traccia di β perpendicolare alla prima traccia di λ. Si determina la generatrice d’intersezione tra β ed il cono; si determina la retta d’intersezione m tra β e λ; infine, il punto d’intersezione tra le due rette individua il vertice M della parabola. come i punti notevoli della parabola sono il vertice. La retta m rappresenta l’asse della parabola. Per determinare un punto generico della parabola si può ripetere l’operazione precedente utilizzando un altro piano ausiliario passante per l'asse di K, e con questo piano sezionare sia il cono sia λ e in ultimo individuare il punto cercato come intersezione delle due sezioni trovate. osservazioni In considerazione del fatto che due piani sono tra loro paralleli se ciascun piano contiene due rette parallele all’altro piano. E questo può essere risolto mediante un altro concetto: una retta e’ parallela ad un piano se la retta e’ parallela ad una retta del piano. Secondo tale considerazione e con riferimento all'esempio in questione non e’ possibile costruire un piano di luce passante per una data retta r in modo che sia parallelo alla generatrici g del cono. Per cui, per impostare questo problema si stabilisce inizialmente un punto P e poi una volta che stato definito il piano di luce passante per P verrà scelto un altro punto appartenete a lamda per definire la retta r. Si fa notare che una volta che stato costruito il piano di luce λ parallelo alla generatrice g del cono, la scelta di qualsisi raggio di luce appartenente a λ, non cambia i risultati delle ombre ottenute, ma modifica solo la posizione dell’ombra P* del estremo P lungo la prima traccia di λ . Inoltre, e poiché per semplicità stata presa la retta r in posizione particolare, parallela alla generatrice g, bisogna sottolineare il fatto che tutte le rette appartenenti a λ producono la stessa ombra. ovvero presa una altra retta n appartenente a λ , l’ombra di n coincide con l’ombra di r sia sul cono sia su π1 العربية: ظل خط مستقيم على مخروط كقطع مكافئ ناتج من تقاطع بين مستوى الضوء المار بالخط والمخروط مثال 2: ظل خط على سطح مخروطي كقطع مكافئ ظل خط مستقيم على مخروط كقطع مكافئ ناتج من تقاطع بين مستوى الضوء المار بالخط والمخروط عمليات ما قبل النمذجة عمليات ما قبل النمذجة الهادفة إلى إنشاء الكيانات المذكورة يمكن أن تكون كالتالي: نرسم دائرة Δ على مستوى الإسقاط الأول كقاعدة للمخروط K. نرسم من مركز Δ خط رأسي a كمحور دوران للمخروط. ونثبت علية نقطة V كقمة للمخروط. نعين الراسم g, من K, بتمرير خط بالقمة V وبنقطة G من القاعدة . لرسم خط r موازي للراسم g، نعيين نقطة T'r على 1π كأول اثر للخط r ومنة نرسم المسقط الأول r1 للخط r بحيث يكون موازي للمسقط الاول g1 للراسم g. نرسم خط رأسي من نقطة P1 من r1 ونعيين علية نقطة P, ثم نرسم الخط r بتوصيل النقطتين T'r P. من أجل رسم شعاع الضوء l نعتبر r كخط أقصى انحدار لمستوى الضوء, وبذلك نرسم الأثر الأول لمستوى الضوء λ عمودي على الإسقاط الاول r1. وبما ان ظل خط على مستوى تحدد كتقاطع بين هذا المستوى ومستوى الضوء المار بالخط, لذلك في هذه الحالة الأثر الأول t'λ للمستوى λ يتطابق مع ظل الخط r . وأخيرا نعيين الظل P* للنقطة P على t'λ ومن ثم بوصل النقطتين P* P نجد اتجاه شعاع الضوء L الاسقاط الاول l1 لهذا الشعاع يمر بالنقطتين P1 P*, . النمذجة التلقائية نشرع بتوليد نموذج المخروط والظلال الساقطة والذاتية للمخروط والخط . لتوليد المخروط نعيين المثلث VV1G كشكل راسم للمخروط , باختيار الخط V1-V كمحور للدوران, والقيمة 360 كزاوية للدوران. لتوليد ظلال المخروط والخط r نعيين الخط P-P* كاتجاه لمصدر ضوء لانهائي. تحليل المفاهيم والتقنيات بعد الانتهاء من إعداد النماذج المعنية لهذه المسألة ، نشرع الى المرحلة الأخيرة لتحليل المفاهيم والتقنيات المتعلقة بالظلال المنشئة تلقائياً. القطع المكافئ يتم الحصول على القطع المكافئ بقطع مخروط ثنائي بمستوى مواز لراسم من رواسم المخروط. في هذه الحالة ، للحصول على ظل الخط r كقطع مكافئ يجب أن يكون مستوى الضوء λ موازي لراسم المخروط g. للتحقق من نوع القطع المخروطي، نمرر بقمة المخروط K مستوى مساعد γ, ووفقاً لميلان هذا المستوى بالنسبة لرواسم المخروط، المقطع يمكن أن يكون ، على التوالي: - قطع ناقص عندما يكون γ غير موازي لرواسم K ؛ وهذا يعني ان λ يقطع جميع رواسم K. - قطع مكافئ، إذا كان γ يقطع جميع رواسم K باستثناء راسم واحد والذي يمثل محور القطع المكافئ؛ - مقطع زائد عندما γ يقطع جميع رواسم المخروط باسثناء راسمان واللذان يمثلان اتجاه الخطان المقاربان للمقطع الزائد توازي بين خط ومستوى ظل خط مستقيم على مخروط يكون قطع مكافئ إذا كان مستوى الضوء موازي لراسم من رواسم المخروط. ينبغي وضع في الاعتبار ان مستوى λ يكون موازي لخط g, إذا كان هناك خط r ينتمي الى λ موازي للخط g. في هذة الحالة يراد إنشاء مستوى ضوء λ موازي للراسم g للمخروط. بهذه الغاية نعيين نقطة P على شعاع الضوء l ومنة نمرر خط موازي للراسم g. نحدد الاثر الاول للمستوى λ (متطابق مع الظل r* للخط r بتوصيل الاثر الاول T’r للخط r مع الأثر الأول (متطابق مع الظل P*) لشعاع الضوء المار بالنقطة P. نقاط هامة لتحديد قمة القطع المكافئ, نمرر بمحور المخروط مستوى β عمودي على مستوى الضوء λ (المار بالخط r). الاثر الاول لβ يمر بالاسقاط الاول V1 لقمة المخروط ويكون عمودي على الاثر الاول ل λ. نحدد راسم التقاطع بين β والمخروط؛ ونحدد خط التقاطع m بين المستويات β و λ . وأخيرا ، نجد قمة القطع المكافئ كنقطة تقاطع M بين الراسم والخط m. الخط m يمثل محور القطع المكافئ. لتحديد نقطة عامة للقطع المكافئ يتم تكرار العملية السابقة باستخدام مستوى مساعد أخر بحيث يمر بمحور المخروط. نحدد تقاطع المستوى المساعد مع المخروط ومع λ لايجاد بالتوالي الراسم d والخط b. وأخيرا نجد نقطة المطلوبة كتقاطع بين الخطين d و b . ملاحظات في ضوء حقيقة أن مستويان يكونان متوازيان إذا كان عل كل مستوى منهما يوجد خطين متوازيين للمستوى الأخر. وبما أن خط يكون موازي لمستوى إذا كان موازي لخط من المستوى, فأنة غير ممكن, بالإشارة إلى المثال المعني, تحديد مستوى ضوء مار λ بخط معطي r بحيث يكون موازي لراسم المخروط. وبالتالي ، لإعداد هذه المسألة ينبغي أولا تحديد نقطة P ومن ثم, بمجرد تعريف أي مستوى ضوء λ مار بالنقطة P , يمكن اختيار نقطة ثانية من λ لإيجاد الخط r. ينبغي الأخذ في الاعتبار أنه بمجرد إيجاد مستوى الضوء λ موازي لراسم مخروط ، عملية اختيار أي شعاع الضوء من بين العدد اللانهائي من الخطوط المنتمية للمستوى λ ، لا تغير نتائج الظل التي تم الحصول عليها، ولكنة يُغير فقط موضع ظل النقط P على طول الاثر الاول للمستوى λ، بالإضافة إلى ذلك وبما أنة تم أخذ الخط r في وضع خاص: موازي للراسم g ، ينبغي التأكيد على حقيقة أن جميع الخطوط المنتمية إلى المستوى λ تنتج نفس الظل. مثلاً إذا أخذنا خط آخر n منتمي إلى λ ، ظل n يتطابق مع ظل الخط r على كل من سطح المخروط ومستوى الإسقاط الأول π1.
Source	Own work
Author	Hasanisawi

هذا الرسمة تم إنشائها وتحميلها من قبل المهندس المعماري حسن العيسوي

Questa immagine opera dell'architetto Hasan ISAWI Sito: http://assex.altervista.org/geomtr-1.htm

Autorizzazione accordata : OTRS #2006051010012313

Palestina libera, rivoluzione fino alla vittoria

Ombra di un cerchio su un cilindro come intersezione tra due cilindri- Shadow of a circle on a cylinder as an intersection between two cylinders- ظل دائرة على اسطوانة كتقاطع بين اسطوانتين

  الدكتور حسن العيسوي

https://www.researchgate.net/profile/ Hasan-Isawi

Italiano: Ombra di un cerchio su un cilindro come intersezione tra due cilindri

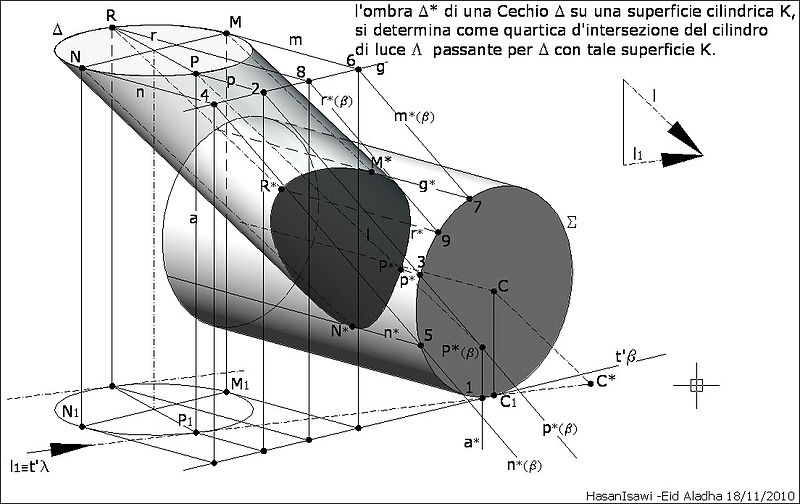
L’ombra di una conica su una superficie curva può essere determinata come intersezione tra due quadriche Per esempio l’ombra di una circonferenza su un cilindro può essere determinata come intersezione tra due cilindri, di cui uno formato dai raggi luminosi passanti per I punti della circonferenza. Come stato affrontato nel paragrafo riferito all’incidenza tra superfici, l’intersezione tra cilindri viene determinata con l’utilizzo di piani ausiliari aventi giacitura parallela a gli assi dei due cilindri. Per inciso e dato che i due assi dei due cilindri in questione sono sghembi, si prende un punto di un asse e si fa passare una retta parallela all’altro asse, in questo modo si ha due rette incidenti che individuano la giacitura di un piano. Allora, quando si dice piani con la stessa giacitura vuole dire che sono paralleli tra loro, e quando si dice che sono paralleli ai due assi significa che ciascun piano di questi contiene due rette paralleli a gli assi dei due cilindri. Ciascun piano ausiliario taglia I due cilindri secondo generatrici che possono intersecarsi rispettivamente in punti formanti una curva 3D detta quartica d’intersezione tra I due cilindri. Per esempio (fig.--) la determinazione dei punti notevoli, come quelli della massima M* e minima quota N* della quartica, e quelli P* e R* della larghezza massima della stessa, possono essere ottenute con procedimenti grafici che sono utili anche quando tale quartica viene generata in automatico, altrimenti, per chi non ha dimestichezza con al geometria descrittiva, si cerca di individuarli a tentativi, e questo non e' un metodi scientifico su cui contare. Per ottenere ad esempio l'ombra P* del punto P che e' uno dei due punti di "larghezza massima della quartica", si procede cosi: si fa passare per P una retta p parallela all'asse del cilindro orizzontale K, in questo modo la sua ombra p* sarà parallela allo stesso asse di K. si determina il punto d'intersezione 2 tra la retta p e il piano β della direttrice di K. Il punto 2 rappresenta già uno dei due punti ombra della retta p sul piano β. l'altro punto ombra P*(β) di P su β, si determina come intersezione del raggio luminoso passante per P con β. tecnicamente, per trovare P*(β) si fa passare per P un raggio luminoso l e per questo un piano di luce λ, in cui prima traccia di λ coincide con la prima proiezione l1 di l. Si determina l'ombra della retta verticale a passante per P, come retta d'intersezione tra i piani β e λ, e poi si individua l'ombra p*(β) nel punto comune alle rette a* ed l. Unendo P*(β) con il punto 2, si individua l'ombra p*(β) di p sul piano β. Si individua il punto 3 come intersezione di p*(β) e la direttrice Σ del cilindro orizzontale. il punto 3 rappresenta un punto ombra della retta p sulla superficie del cilindro K, e poiché p e' parallela all'asse di k, dal punto 3 vi si traccia la parallela. In ultimo si individua l'ombra P* di P sulla superficie di K come intersezione del raggio luminoso passante per P con l'ombra p* della retta p sulla stessa superficie. Analogamente, si determinano gli altri punti notevoli R*, M*, N*, della quartica-ombra. Le operazione in questi casi sono' più rapide dato che le ombre (g* r* n* p*) di rette parallele (g r n p) su un stesso piano β rimangono parallele tra loro, per cui tracciati le rette orizzontali m,r,n passanti rispettivamente per i punti M,R,N, ed individuati i loro punti 6,8,4 con la retta orizzontale g (intersezione tra il piano orizzontale della circonferenza ∆ con il piano β), si disegnano le ombre m*(β), r*(β), n*(β) in modo che siano parallele all'ombra p*(β) della retta p su β. dai punti 7, 9, 4, d'incontro tra Σ con le ombre m*(β), r*(β), n*(β), si tracciano le rette parallele all'asse e cosi si individuano i punti-ombra M*, R*, N*, sulla superficie del cilindro orizzontale, come intersezione dei raggi luminosi passanti per i punti oggettivi M, R, N, con le rette-ombra m*, r*, n*. Il punto-ombra M* rappresenta il punto di massima quota che appartiene ad uno dei due piani di luce tangenti la circonferenza oggettiva ∆. l'altro piano di luce tangente ∆ individua il punto N* di minima quota della quartica. gli altri due punti-ombra R* e P*, appartengono a due piani di luce verticali tangenti ∆ e rappresentano la massima larghezza della quartica.

 العربية: ظل دائرة على اسطوانة كتقاطع بين اسطوانتين___________

 ظل قطع مخروطي على سطح منحن يمكن ان يحدد كتقاطع بين أسطح ثنائية (quadrics). على سبيل المثال ، يمكن تحديد ظل دائرة على اسطوانة كتقاطع بين اسطوانتين ، واحدة منهما تتكون من أشعة الضوء التي تمر بنقاط تلك الدائرة. كما نوقش في الفقرة المتعلقة بالتقاطع بين السطوح الثنائية ، تم تحديد التقاطع بين الاسطوانتين من خلال استخدام مستويات مساعدة موازية لمحاور الاسطوانات. عملياً, وبما أن محاور الاسطوانتين المعنية (شكل --) متخالفة (skew lines)، نأخذ نقطة من محور ونمرر به خط مواز للمحور الآخر ، وبذلك لدينا خطين متقاطعين التا يحددان مستوى. فعندما نقول مستويات بنفس الميلان يعني انها موازية لبعضها البعض ، وعندما نقول أنها موازية لمحاور الاسطوانتين يعني ان كل مستوى يحتوي على خطين موازيين لتلك المحاور. كل مستوى مساعد يقطع كل اسطوانة منهما وفقاً لخطين, نقاط التقاطع بين الخطوط يمكن ان تشكل منحنى ثلاثي الابعاد , الذي يسمى منحنى رباعي (quartic)كتقاطع بين اسطح ثنائية. على سبيل المثال (الشكل --) يمكن تحديد النقاط الهامة للرباعي ، مثل نقطة الحد الأقصى M* والحد الأدنى N* للرباعي, والنقاط P* وR* لأقصى عرض لنفس الرباعي ، من خلال انشاءات الهندسة الوصفية التي هي ضرورية خصوصاُ في الحالات التي يتم إنشاء مثل هذا الرباعي تلقائيا بواسطة الحاسوب. خلاف لذلك، وبالأخص لؤلئك الذين ليس لديهم خلفية نظرية بعلم الهندسة الوصفية، سيكون هناك العديد من المحاولات للوصول الى نتائج تقريبية في العثور على نقاط هامة لرباعي تقاطع بين أسطح ثنائية. وهذه لا يمكن أن تعتبر طرق علمية ولا عملية يمكن الاعتماد عليها للتحكم في الفراغ الهندسي. على سبيل المثال ، للحصول على ظل P* للنقطة P , واحدة من نقطتين أقصى عرض لمنحنى التقاطع الرباعي، ينبغي المضي قدما كما يلي : نمرر بالنقطة P خط p موازي لمحور الاسطوانة الافقية K التي تتلقى الظل. في هذة الطريقة, الظل P* على سطح K سيكون مواز لنفس المحور. نحدد نقطة التقاطع 2 بين الخط p والمستوى الرأسي β للقاعدة Σ ( واحدة من قاعدتين الاسطوانة K). النقطة 2 تمثل ظل نقطة للخط p على المستوى β. نحدد ظل P*(β) لنقطة آخرى P للخط p على β, كتقاطع بين شعاع الضوء l المار بالنقط P والمستوى β . عملياً نمرر بالنقطة P شعاع الضوء l . وبهذا الشعاع نمرر مستوى رأسي λ , بحيث اثرة الاول يتطابق مع الاسقاط الاول l1 للشعاع l . نحدد خط التقاطع a* بين المستويات λ وβ ، وهكذا نعثر على الظل p*(β) كتقاطع بين خط التقاطع a* والشعاع l. بتوصيل النقطة p*(β) مع النقطة 2 نحصل عل الظل p*(β) للخط p على المستوى β . نعثر على النقطة 3 كتقاطع بين الظل p*(β) للخط p والقاعدة Σ للاسطوانة الأفقية. K النقطة 3 تمثل ظل نقطة للخط p على سطح الاسطوانة K. ومنذ ان p موازي لمحور K ، فمن النقطة ، نرسم الظل p* موازي لهذا المحور. وأخيرا نعثر على الظل P* للنقطة P على سطح K , كتقاطع بين شعاع الضوء المار بالنقطة P والظل p* للخط p على نفس السطح. وبالمثل ، يتم تحديد النقاط الهامة الأخرى R*, M*, N*، للمنحنى الرباعي كظلال للنقاط R, M, N المنتمية الى الدائرة ∆. عمليات الرسم في هذه الحالات عادة ما تكون اسرع لان الخطوط (g r n p) متوازية بينها وهذا يعني ان ظلها على المستوى β ستكون متوازية بينها. عملياً نرسم الخطوط m,r,n الموازية لمحور الاسطوانة والمارة بالنقاط M,R,N, للدائرة ∆. حيث هذة الخطوط تقابل المستوى β في النقاط 6,8,4, نرسم الظلال m*(β), r*(β), n*(β) بشكل موازي للظل p* للخط p الذي وجدناة سابقاُ. من نقاط 7, 9, 4 تقابل القاعدة Σ مع هذة الظلال نرسم خطوط موازية لمحور الاسطوانة المتلقية, وهكذا نجد نقاط الظل M*, R*, N*, على سطح الاسطوانة كتقاطع بين الظلال m*, r*, n* وخطوط الاشعة المارة بالنقاط M, R, N. نقطة الظل M* تمثل نقطة اقصى ارتفاع للمنحنى الرباعي والتي تنتمي الى واحد من المستويين المتماسين الدائرة Δ. المستوى الاخر يحتوي على نقطة أدنى ارتفاع للرباعي . نقاط الظل الآخرى التي تمثل أقصى عرض للرباعي ، تنتمي إلى مستويين راسيين متماسيين الدائرة Δ . 

Date 18 November 2010 Source Own work Author Hasanisawi هذا الرسمة تم إنشائها وتحميلها من قبل المهندس المعماري حسن العيسوي Questa immagine opera dell'architetto Hasan ISAWI Sito: http://assex.altervista.org/geomtr-1.htm Autorizzazione accordata : OTRS #2006051010012313 Palestina libera, rivoluzione fino alla vittoria Licensing

Ombre come sezioni coniche- Shadows as conic sections. ظل خط على سطح مخروطي كمقطع مخروطي

 الدكتور حسن العيسوي
https://www.researchgate.net/profile/ Hasan-Isawi

Description	Italiano: Ombre come sezioni coniche. L’ombra di una retta su una superficie conica e’ una conica (eventualmente degenere). Secondo la giacitura del piano di luce ,passante per tale rette, rispetto alle generatrici del cono, l'ombra della retta può essere rispettivamente: Un ellisse, quando il piano di luce λ taglia tutte le generatrici del cono K Un parabola quando il piano λ seziona K ed e’ parallelo ad una generatrici di K Una iperbole quando λ seziona K ed e’ parallelo a due generatrici di K Un punto quando il piano di luce passa per il vertice di K Una retta quando il piano di luce tange la superficie di K Ombra iperbolica di una retta su un cono Anche in questo caso, come gli altri casi delle coniche ottenute come sezioni di un un cono quadrico con un piano, l'iperbole si può ottenere nello spazio come ombra di una retta sul cono, nella condizione in cui tale retta debba appartenere ad un piano che passa per il vertice del cono e che lo seziona secondo due generatrici. Si fa notare che le direzione di queste generatici sono paralleli alle direzioni degli asintoti dell’iperbole. Premodellazione La fase di premodellazione (o la fase di costruzione geometriche preparatorie) , consiste nel determinare degli elementi minimi indispensabili per la generazione dei modelli e in particolare la determinazione delle reciproche posizioni di un cono di rotazione K e di un piano di luce λ parallelo a due generatici di K. Elementi notevoli del cono Gli elementi notevoli che permettono di generare un cono di rotazione sono la generatrice g e l’asse a, che bisogna che siano i lati di un triangolo rettangolo per poter generare il modello solido del cono. Si fa ricordare che la modellazione solida, Come stato citato nel paragrafo dedicato, si differenzia dalle altre modalità Wireframe e Mesh, per tanti vantaggi che offre, quali la possibilità di determinarvi l’intersezione con un piano con un solido, la possibilità di svuotare il solido lasciando un spessore al proprio involucro (solidedit, shell), la possibilità di determinarvi fisicamente le proiezioni ortogonali su un piano (solprof). Individuazione del piano di luce Bisogna sottolineare il fatto che il modo più rapido per definire un piano λ secante un cono K e parallelo a due generatrici di K, e’ quello di assumere un piano ausiliario che passa per il vetrice di K e che lo seziona secondo due generatrici b d. In questo modo qualsiasi piano λ parallelo a γ e secante il cono produce come sezione una iperbole avente asintoti paralleli alle due generatrici. Questi operazioni di costruzioni geometriche preparatorie possono essere eseguite sia nello spazio che nel piano con il classico metodo di Monge. Si fa ricordare che due piani sono paralleli tra loro se ciascun piano contiene due rette parallele all’altro piano. E questo discende dal concetto di parallelismo tra una retta ed un piano, secondo il quale una retta r e’ parallela ad un piano γ se e’ parallela ad una retta f di γ . Per inciso, si individuano le due generatrici b d come sezione di un piano γ con il cono e poi per il punto dato P si disegna la retta r parallela ad una retta f appartenente al piano γ . tecnicamente si procede come di seguito: Si fa passare per il vertice V del cono un piano γ secante il cono secondo due generatrici b d. Si fa notare che in questo modo abbiamo già deciso la giacitura del piano di luce, dato che i piani λ e γ debbono essere tra loro paralleli per costruzione, si sceglie una retta f appartenente al piano γ . si fa passare per P una retta r parallela alla retta f. Si fa ricordare che due rette sono paralleli ta loro quando ciascuna retta ha due proiezioni parallele alle proiezioni omonime dell'altra retta. Per inciso, per P si fa passare r parallela ad f e per P1 si disegna r1 parallela ad f1. si individua la direzione del raggio luminso l, detrminando il punto d’intersezione V* di una retta apartenete a gamma e passante per il vertice V con il piano della base del cono. Si fa notare che una volta definito il piano di luce λ, che per costruzione passa per r ed e' parallelo alle due genratrici b d del piano γ, la scelta di qualsiasi raggio luminoso l passante per P e appartenente a λ non modifica il risultato della sezione iperbolica ottenuta come sezione di λ con il cono. العربية: ظل خط على سطح مخروطي كمقطع مخروطي ظل خط مستقيم على سطح مخروطي يمكن ان يكون قطع مخروطي (ربما متدهور ( وفقا لميلان مستوى الضوء λ (المار بالخط) بالنسبة لرواسم المخروط ، القطع المخروطي يمكن أن يكون على التوالي : قطع ناقص ، عندما مستوى الضوء λ يقطع جميع رواسم سطح المخروط K. قطع مكافئ عندما مستوى الضوء λ يوازي واحد من رواسم K قطع زائد عندما λ يوازي اثنين من رواسم K نقطة عندما λ يمر بقمة K خط عندما λ يلامس سطح K ظل خط على مخروط كقطع زائد في هذة الحالة, كما في حالات القطع المخروطية الأخرى التي واجهناها سابقاً ، يتم الحصول على مقطع مخروطي كظل لخط على مخروط. ظل الخط يكون قطع زائد اذا كان الخط موازي لمستوى مار بقمة المخروط وقاطعة وفقاً لراسمين. ينبغي معرفة ان الخطوط المقاربة (Asymptote) للقطع الزائد تكون موازية لتلك الرواسم. مرحلة ما قبل النمذجة مرحلة ما قبل النمذجة (أو الانشاءات الهندسية التحضيرية) ، تكمن في تحديد الحد الأدنى من العناصر اللازمة لانشاء النماذج اللازمة (مخروط ومستوى ضوء) ومواضعهم المتبادلة (توازي, تقاطع العناصر الهامة للمخروط الدوراني العناصر الرئيسية التي تسمح بتوليد المخروط الدوراني تتكون من راسم السطح ومحور الوران. والتي ، التي يجب ان تكونان ضلعين لمثلث قائم الزاوية من اجل توليد نموذج صلب للمخروط. وتجدر الإشارة إلى أن النمذجة الصلبة ، كما ذكر في الباب ذو الصلة، تتميز عن طرق النمذجة الاخرى ( السلكية Wireframe- والسطحيةMesh-) باستحقاقات عديدة مثل القدرة على توليد مقاطع مستوية او فراغية لمجسمات صلبة ، او تجويفها بترك سمك معين للجدار الخاصة بها ، او القدرة على توليد اسقاطات متعامدة لها على مستوى معين (solid profiles) تحديد مستوى الضوء وينبغي التأكيد على أن أسرع طريقة لتحديد مستوى λ يقطع مخروط وفقاً لقطع زائد هي في استخدام مستوى مساعد γ يمر بقمة المخروط ويقطع المخروط وفقاً لراسمي, بهذه الطريقة ، أي مستوى λ موازي للمستوى γ يقطع المخروط وفقاً لقطع زائد. يمكن تنفيذ هذه العمليات التحضيرية في كل من الفراغ بواسطة اسقاطات منفردة او على المستوى بواسطة طريقة مونج الكلاسيكية. ينبغي الاخذ في الاعتبار ان مستويان يكونان متوازيان لبعضها البعض إذا كان كل مستوى يحتوي على خطين متوازيين للمستوى الاخر. وهذا يعتمد على مفهوم اخر وهو التوازي بين خط ومستوى، والذي بموجبه خط r يكون موازي لمستوى γ عندما يكون موازي لخط على المستوى γ. وبالاشارة الى المثال المقترح، يتم أولا تحديد المستوى γ الذي يقطع المخروط وفقاً لراسمين ومن ثم من النقطة المعطية P يتم رسم خط r موازي لخط f ينتمي للمستوى γ. تقنياً نشرع على النحو التالي : يتم قطع المخروط بمستوى γ مار بقمة الرأس وقاطع المخروط وفقاً لراسمين b و d. تجدر الإشارة إلى أنه في هذة الطريقة قد حددنا بالفعل ميلان مستوى الضوء ، منذ ان المستويات γ و λ يجب أن يكونوا متوازية مع بعضها البعض كشرط لحل هذة المسألة. يتم اختيار خط f تنتمي إلى المستوى γ. ومن ثم نمرر بالنقطة P الخط r بحيث يكون موازي للخط f . تجدر الإشارة إلى أن خطان يكونان متوازيان لبعضها البعض اذا كان لكل خط اسقاطين متوازيين بالتوالي لاسقاطين الخط الاخر. أي من النقطة P نمرر الخط r موازي للخط f ، ومن P1 نمرر r1 مواز للخط f1. * يتم ايجاد اتجاة شعاع ضوء كخط ينتمي الى المستوى γ ويمر برأس المخروط ويقطع مستوى القاعدة في النقطة V*. ينبغي الاخذ في الاعتبار انة بمجرد تحديد المستوى λ , الذي يوازي للراسمان المنتميان للمستوى γ , اختيار أي شعاع ضوء l مار بالنقطة P ومنتمي ل λ لا يغير القطع الزائد الناتج من تقاطع λ والمخروط.
Date	07/11/2010
Source	Own work
Author	Hasanisawi

هذا الرسمة تم إنشائها وتحميلها من قبل المهندس المعماري حسن العيسوي

Questa immagine opera dell'architetto Hasan ISAWI

Sito dell'autore: http://assex.altervista.org/geomtr-1.htm

Autorizzazione accordata : OTRS #2006051010012313

La liberazione della Palestina e' solo questione di tempo. Rivoluzione fino alla vittoria.

 

Sheikh Jarrah (quartiere palestinese)

Da Wikipedia, l'enciclopedia libera.

Jump to navigationJump to search

Sheikh Jarrah è un villaggio palestinese affiliato al Governatorato di Gerusalemme, situato sul lato orientale della città di Gerusalemme, occupato dagli israeliani nella guerra del 1967. Oggi è uno dei quartieri di Gerusalemme est.

Ingresso al quartiere di Sheikh Jarrah, Gerusalemme Est.

Il quartiere di Sheikh Jarrah a Gerusalemme ha preso il nome dal principe Hussam al-Din al-Jarrahi (medico di Salah Al-Din Al-Ayyubi, ed è minacciato da un annunciato piano di insediamento israeliano, che include la costruzione di 200 unità di alloggi residenziali per coloni ebrei, nel mezzo di questo quartiere arabo.

Il quartiere di Sheikh Jarrah si trova sul lato orientale della Città Vecchia di Gerusalemme fuori le mura. Il quartiere è stato fondato a Gerusalemme nel 1956 in base a un accordo firmato tra l'UNRWA e il governo giordano, all'epoca ospitava 28 famiglie palestinesi cacciate dalle loro case che sono state occupate da Israele nel 1948.

I coloni sionist

Riferimenti

1. ^ Sheikh Jarrah..un quartiere invaso da insediamenti e telecamere- 27/2/2017