Gaspard Monge,
Géométrie descriptive,
1a ed.
1794-95. 6a ed.
1837
Gaspard Monge è considerato l'iniziatore della
geometria pura moderna. Monge fu tra i fondatori dell'École Politecnique, una
delle strutture educative (dedicate all'istruzione superiore) sorte dalla
Rivoluzione Francese. Un insegnamento nuovo introdotto da Monge fu quello della
geometria descrittiva. L'opera di Monge, Géométrie Descriptive (1794-95),
raccoglie le lezioni tenute all'École Normale dell'anno terzo.
Contiene il metodo della doppia proiezione ortogonale, ossia il metodo ancora in
uso nel disegno geometrico, per cui da due proiezioni su due piani ortogonali
(pianta e alzata), uno dei quali ribaltato sull'altro, si ottengono le proprietà
della figura spaziale e viceversa.
L'insegnamento di Monge all'École
Politecnique formò nuove generazioni di ingegneri e stimolò la rinascita della
geometria sintetica che ebbe uno sviluppo straordinario nella prima metà
dell'Ottocento.
Il teorema di Monge qui riportato è un esempio in cui la
dimostrazione di un teorema di geometria piana è più semplice facendo uso della
geometria dello spazio.
Tre cerchi qualunque del piano considerati a due a due hanno le tangenti
comuni che si incontrano in tre punti allineati.
Se si considerano le tre sfere di cui questi cerchi sono i cerchi massimi e
un piano tangente esternamente a tutte e tre, questo piano sarà tangente
esternamente anche ai tre coni circoscritti alle sfere considerate a due a
due, e passerà per i tre vertici D, E, F.
Ma questi tre vertici sono pure nel piano dei tre centri, dunque si trovano
all’intersezione di due piani diversi, e per conseguenza sono in linea
retta.
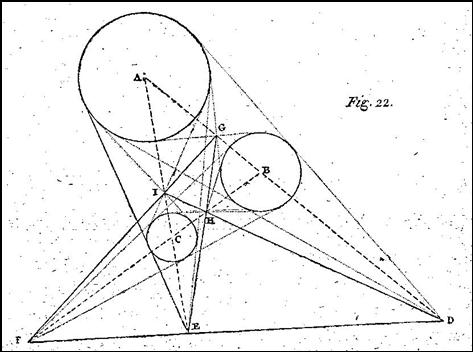
Per trovare il centro di similitudine di due cerchi
basta fissare ad arbitrio un raggio su una delle due circonferenze e
tracciare il raggio parallelo nell'altra. La retta congiungente gli estremi
di questi due raggi sulla circonferenza interseca la retta dei centri nel
centro di similitudine.
FAQ: domande degli studenti
GPM - Programma e tavole delle esercitazioni
Revisione geometria descrittiva. venerdi 20/10, ore 15:00
Geometria descrittiva / laboratorio /Consegne composizione Volumi 01 e 02
regole del disegno esecutivio by roberto veneziani
superfici rigate
CHATtare
Risorsa
Glossario (geometria descrittiva)
attività intercorso
isawi hasan
Documentazione di Moodle per questa pagina