|
- last update 25-07-2007
|
Elicoidi
|
|
|
Approssimare un elicoide conica circolare
|

|
Elicoide prismatica regolare
|
 |
Elicoide conica circolare a generatrice variabile
|
 |
|
|
|
|
|

|
Tav.11/3_(consigliabile)
Modellazione solida di Rampe elicoidali consecutive ( a cilindri di
rotazione)
Dislivello= 3 M
Area d'ingombro= 74.66
Pendenza= 9%
|
 |
Tav.11/2: Modellazione solida di due rampe elicoidali consecutive e
contigue, con pendenza del 8%. Il dislivello da superare è di 3 metri.
|
 |
Tav.11/1: Scala a chiocciola circolare e retta
Scala a chiocciola ottenuta come modellazione
solida. Il quale è stata possibile attraverso una rapida approssimazione
della superficie rigata (intradosso della scala in esame) con un
numero limitato di piani
|
 |
|
|
|
Rampa elicoidale ottenuta
come modellazione di superfici. Gli inconvenienti di questo tipo di
modellazione, almeno in AutoCAD, consistono nell'impossibilità di poter
eseguire operazioni di modifica, come quelle Booleane ( intersezione,
sottrazione ed unione).
|
 |
|
|
|
Modellazione solida di una rampa elicoidale circolare e
retta. in questo caso le superfici rigate dell'intradosso e quella
dell'estradosso, sono stati ottenute come sezione piane di un numero
limitato di prismi aventi basi triangolari.
|
 |
|
|
|
|
Elica sferica tangenti due rette sghembe
Dati
due rette sghembe r ed s. Vi si vuole determinare il percorso piu breve in modo che
passi per un punto A di r e che risulti tangente l'altra
retta s.
|
 |
|
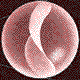
Elica sferica, detta comunemente otto volante, è un
curva generata da un circonferenza meridiana, mentre questa esegue, contemporaneamente,
due rotazioni cicliche ( il punto di partenza coincide con il punto
d'arrivo), che sono, rispettivamente, una intorno all'asse verticale della propria
sfera e l'altra intorno al centro della stessa circonferenza.
Nota:
la sopradetta elica sferica, si può ottenere come intersezione tra due
cilindri di rotazione con una sfera ( Vedi
finestra di Viviani )
|
 |
|
Elica sfericilindrica ottenuta con un appropriato accoppiamento di due finestra di
Viviani simmetriche tra loro.
|
 |
|
Elica sfericoncoidica: ottenuta con un appropriato accoppiamento di due
finestre di viviani, ottenute a loro volta, come intersezione di due coni ellittici,
tra loro simmetrici, con un stessa sfera.
|
 |
Dati due coppie di rette a,b ed c,d, (a//b ed appartenenti,
rispettivamente, a due piani alpha e beta tra loro paralleli. in cui risulta
che a // b ed c//d, e la distanza tra a b è uguale a quella tra cd.
|
 |
Si vuole determinare un rampa elicoidale che permette di
raccordare, due a due, le rette date e che abbia, rispettivamente,
larghezza costante e pendenza del 8%
( vedi Esempio).
|
 |
|
Studio sui possibili raccordi tangenziali tra coniche non
complanari (rette e circonferenza)
|
 |
|
Raccordi elicoidali tra coniche sghembe (retta e
circonferenza)
|
 |
 |
|
Geometry Dance
|
 |
|
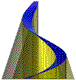
copertura delimita da una elica concoidica che stata ottenuta come quartica d'intersezione di
un cono di rotazione con un cilindro policentrico.
|
 |
|
Rampa elicoidale concoidica,
ha la
proprietà di decentrarsi rapidamente, per cui come rampa pedonale, rispetto a quella cilindrica
ed a parità di pendenza, ha il vantaggio di non avere problemi di altezza
minima (M 2.40) nei spazi percorribili.
|
 |
 |
|
|
|
|
Eliconcoidi
|
 |
ليست هناك تعليقات:
إرسال تعليق